异或和(xorsum)
【问题描述】
小可可在五年级暑假开始学习编程,编程语言中有一种“按位异或(xor)”的运算引起了他的莫大兴趣。于是,他思考这样的一个问题:给一个长度为 n 的整数序列 A,如 何计算出满足下列两个条件的整数对 (l, r) 的数量。
1、1≤l≤r≤n;
2、Al xor Al+1 xor … xor Ar = Al + Al+1 + … + Ar
这里的 xor 就是按位异或(C 或 C++语言中“按位异或”运算符为^),求 a xor b 的原理是:将 a 和b 转换为二进制,如果 a、b 的二进制表示中对应位置不相同,则异或结果的二进制表示中对应位置为 1,如果 a、b 的二进制表示中对应位置相同,则异或结果的二进制表示中对应位置为 0。例如:计算 10 xor 12,二进制表示 10 是 1010,二进制表示 12 是 1100,10 xor 12 结果的二进制表示是 0110,即为 6。具体为下式:
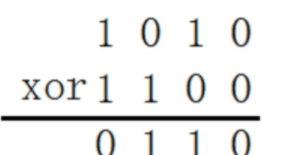
小可可虽然提出了问题,但他自己不会解决,只好又要麻烦你解决啦。
【输入格式】
输入有两行:
第一行一个正整数 n,表示整数序列 A 的元素个数。
第二行有 n 个整数,第 i 个整数 Ai 表示整数序列 A 的第 i 个元素的值。
【输出格式】
输出一行,包括一个正整数,表示满足条件的整数对 (l, r) 的数量。
【输入输出样例 1】
输入
2 5 4 6
输出
【样例 1 解释】
(l, r) = (1, 1)、(2, 2)、(3, 3)、(4, 4)显然满足条件,还有(l, r) = (1, 2)也满足条件,因为 A1 xor A2=2 xor 5=7,而 A1 + A2=2 + 5=7。所以满足条件的整数对 (l, r) 的数量为 5。
【输入输出样例 2】
输入
885 8 1 128 83 32 256 206 639 16 4 128 689 32 8 64 885 969 1
输出:
【数据范围】
对于 20%的数据满足:Ai = 0 (1≤ i ≤n)。
另有 30%的数据满足:1≤ n ≤ 5000。
对于 100%的数据满足:1≤ n ≤ 200000,0≤ Ai ≤ 2^20。