矩阵变幻:
有一个奇幻的矩阵,在不停的变幻,其变幻方式为:数字0变成矩阵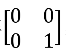 ,数字1变成矩阵
,数字1变成矩阵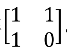 。最初该矩阵只有一个元素0,变幻n
。最初该矩阵只有一个元素0,变幻n
次后,矩阵会变成什么样?
例如,矩阵最初为:[0];矩阵变幻1次后: 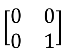 ;矩阵变幻2次后:
;矩阵变幻2次后: 。
。
输入一行一个不超过10的正整数n。输出变幻n次后的矩阵。
试补全程序。
提示:
“<<”表示二进制左移运算符,例如(11)2<<2=(1100)2;
而“^”表示二进制异或运算符,它将两个参与运算的数中的每个对应的二进制位一一进行比较,若两个二进制位相同,则运算结果的对应二进制位为0,反之为1。
#include <bits/stdc++.h>
using namespace std;
int n;
const int max_size = 1 << 10;
int res[max_size][max_size];
void recursive(int x, int y, int n, int t)
{
if (n == 0)
{
res[x][y] = ______(1)______;
return;
}
int step = 1 << (n - 1);
recursive(______(2)______, n - 1, t);
recursive(x, y + step, n - 1, t);
recursive(x + step, y, n - 1, t);
recursive(______(3)______, n - 1, !t);
}
int main()
{
scanf("%d", &n);
recursive(0, 0, ______(4)______);
int size = ______(5)______;
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
printf("%d", res[i][j]);
puts("");
}
return 0;
}
①处应填( )
n%2
0
t
1
②处应填( )
x-step,y-step
x,y-step
x-step,y
x,y
③处应填( )
x-step,y-step
x+step,y+step
x-step,y
x,y-step
④处应填( )
n-1,n%2
n,0
n,n%2
n-1,0
⑤处应填( )
1<<(n+1)
1<<n
n+1
1<<(n-1)