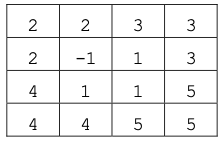
2007年NOIP初赛普及组完善程序：(棋盘覆盖问题)在一个2k × 2k 个方格组成的棋盘中恰有一个方格与其他方格不同(图中标记为 -1 的方格)，称之为特殊方格。现用 L 型(占 3 个小格)纸片覆盖棋盘上除特殊方格的所有部分，各纸 片不得重叠，于是，用到的纸片数恰好是(4k −1)/3。在下表给出的一个覆盖方案中，k=2，相同的3 个数字构成一个纸片。

下面给出的程序是用分治法设计的，将棋盘一分为四，依次处理左上角、右上角、左下角、右下角， 递归进行。请将程序补充完整。

#include <iostream.h>
#include <iomanip.h>

int board[65][65], tile; /* tile为纸片编号 */
void chessboard(int tr, int tc, int dr, int dc, int size)
/* dr,dc依次为特殊方格的行、列号 */
{
    int t, s;
    if (size == 1)
        ① ；
        t = tile++;
    s = size / 2;
    if ( ② )
        chessboard(tr, tc, dr, dc, s);
    } else{
        board[tr + s - 1][tc + s - 1] = t;
        [③];
    }
    if (dr < tr + s && dc >= tc + s)
        chessboard(tr, tc + s, dr, dc, s);
    } else {
        board[tr + s - 1][tc + s] = t;
        ④;
    }
    if (dr >= tr + s && dc < tc + s)
        chessboard(tr + s, tc, dr, dc, s);
    } else {
        board[tr + s][tc + s - 1] = t;
        [⑤];
    }
    if (dr >= tr + s && dc >= tc + s)
        chessboard(tr + s, tc + s, dr, dc, s);
    } else {
        board[tr + s][tc + s] = t;
        [⑥];
    }
}

void prtl(int b[][65], int n) {
    int i, j;
    for (i = 1; i <= n; i++) {
        for (j = 1; j <= n; j++)
            cout << setw(3) << b[i][j];
        cout << endl;
    }
}

void main() {
    int size, dr, dc;
    cout << "input size(4/8/16/64):" << endl;
    cin >> size;
    cout << "input the position of special block(x,y):" << endl;
    cin >> dr >> dc;
    board[dr][dc] = -1;
    tile++;
    chessboard(1, 1, dr, dc, size);
    prtl(board, size);
}