种树(tree)
【题目描述】
你是一个森林养护员,有一天,你接到了一个任务:在一片森林内的地块上种树, 并养护至树木长到指定的高度。
森林的地图有 n 片地块,其中 1 号地块连接森林的入口。共有 n − 1 条道路连接这 些地块,使得每片地块都能通过道路互相到达。最开始,每片地块上都没有树木。
你的目标是:在每片地块上均种植一棵树木,并使得 i 号地块上的树的高度生长到 不低于 ai 米。
你 每 天 可 以 选 择 一 个 未 种 树 且 与. 某. 个. 已. 种. 树. 的. 地. 块. 直. 接. 邻. 接. ( 即. 通. 过. 单. 条. 道. 路. 相. 连.)的地块,种一棵高度为0米的树。如果所有地块均已种过树,则你当天不进行任何 操作。特别地,第 1 天你只能在 1 号空地种树。
对每个地块而言,从该地块被种下树的当天开始,该地块上的树每天都会生长一定 的高度。由于气候和土壤条件不同,在第 x 天,i 号地块上的树会长高 max(bi + x ∗ ci, 1) 米。注意这里的 x 是从整个任务的第一天,而非种下这棵树的第一天开始计算。
你想知道:最少需要多少天能够完成你的任务?
【输入格式】
从文件 tree.in 中读入数据。
输入的第一行包含一个正整数 n,表示森林的地块数量。
接下来 n 行:每行包含三个整数 ai, bi, ci,分别描述一片地块,含义如题目描述中
所述。
接下来 n − 1 行:每行包含两个正整数 ui, vi,表示一条连接地块 ui 和 vi 的道路。
【输出格式】
输出到文件 tree.out 中。 输出一行仅包含一个正整数,表示完成任务所需的最少天数。
【样例 1 输入】
4
12 1 1
2 4 ‐1
10 3 0
7 10 ‐2
1 2
1 3
3 4
【样例 1 输出】
5
【样例 1 解释】
第 1 天:在地块 1 种树,地块 1 的树木长高至 2 米。
第 2 天:在地块 3 种树,地块 1, 3 的树木分别长高至 5, 3 米。
第 3 天:在地块 4 种树,地块 1, 3, 4 的树木分别长高至 9, 6, 4 米。
第 4 天:在地块 2 种树,地块 1, 2, 3, 4 的树木分别长高至 14, 1, 9, 6 米。 第 5 天:地块 1, 2, 3, 4 的树木分别长高至 20, 2, 12, 7 米。
【样例 2】
见选手目录下的 tree/tree2.in 与 tree/tree2.ans。
【样例 3】
见选手目录下的 tree/tree3.in 与 tree/tree3.ans。
【样例 4】
见选手目录下的 tree/tree4.in 与 tree/tree4.ans。
【数据范围】
对于所有测试数据有:1≤n≤105,1≤ai ≤1018,1≤bi ≤109,0≤|ci|≤109, 1 ≤ ui, vi ≤ n。保证存在方案能在 109 天内完成任务
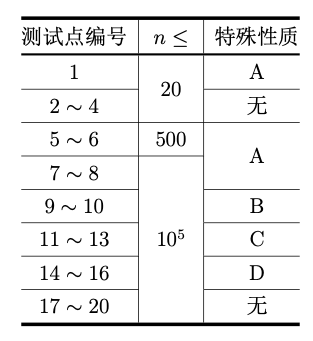
特殊性质A:对于所有1 ≤ i ≤ n,均有ci = 0;
特殊性质B:对于所有1 ≤ i < n,均有ui = i,vi = i+1;
特殊性质 C:与任何地块直接相连的道路均不超过 2 条;
特殊性质D:对于所有1 ≤ i < n,均有ui = 1。