试题名称:奖品分配
班上有 N 名同学,学号从 0 到 N-1 。有 M 种奖品要分给这些同学,其中,第 i 种奖品总共有 ai 个(i=0,1,.....M-1 )。巧合的是,奖品的数量不多不少,每位同学都可以恰好分到⼀个奖品,且最后剩余的奖品不超过1 个(即: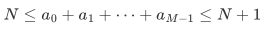 )。
)。
现在,请你求出每个班级礼物分配的⽅案数,所谓⽅案,指的是为每位同学都分配⼀个种类的奖品。只要有⼀位同 学获得了不同种类的奖品,即视为不同的⽅案。⽅便起见,你只需要输出⽅案数对 109+7 取模后的结果即可。
共有 T 个班级都⾯临着奖品分配的问题,你需要依次为他们解答。
输入描述
第一行一个整数 T,表示班级数量。
接下来 T 行,每行若干用单个空格隔开的正整数。首先是两个正整数 N,M ,接着是 M个正整数 。 保证 。
。 保证 。
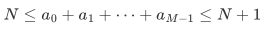
输出描述
输出 T 行,每行一个整数,表示该班级分配奖品的方案数对 109+7 取模的结果。
样例输入 1
1 3 2 3 2 1 2 3 3 2 1 3 4 5 3 3 1
样例输出 1
1 3 2 4 3 20
样例解释1
对于第1 个班级,学号为 0,1,2 的同学可以依次分别获得奖品 0,1,1 ,也可以依次分别获得奖品 1,0,1 ,也可以依次 分别获得奖品 1,1,0 ,因此共有 3 种⽅案。
对于第2 个班级,学号为 0,1,2 的同学可以依次分别获得奖品 0,1,1 ,也可以依次分别获得奖品 1,0,1 ,也可以依次 分别获得奖品 1,1,1 ,也可以依次分别获得奖品 1,1,1 ,因此共有 4 种⽅案。
对于第3 个班级,可以把编号为 1 的奖品分配给 5 名同学中的任意⼀名,共有 5 种⽅案;再把编号为 2 的奖品分配 给剩余 4 名同学中的任意⼀名,共有 4 种⽅案;最后给剩余 3 名同学⾃然获得 0 号奖品。因此,⽅案数为5*4=20。
样例输入 2

样例输出 2

数据规模