密码锁(lock)
【题目描述】
小 Y 有一把五个拨圈的密码锁。如图所示,每个拨圈上是从 0 到 9 的数字。每个 拨圈都是从 0 到 9 的循环,即 9 拨动一个位置后可以变成 0 或 8,

图 1: 密码锁
因为校园里比较安全,小 Y 采用的锁车方式是:从正确密码开始,随机转动密码锁 仅一次;每次都是以某个幅度仅转动一个拨圈或者同时转动两个相邻的拨圈。
当小 Y 选择同时转动两个相邻拨圈时,两个拨圈转动的幅度相同,即小 Y 可以将 密码锁从 0 0 1 1 5 转成 1 1 1 1 5,但不会转成 1 2 1 1 5。
时间久了,小 Y 也担心这么锁车的安全性,所以小 Y 记下了自己锁车后密码锁的 n 个状态,注意这 n 个状态都不是正确密码。
为了检验这么锁车的安全性,小 Y 有多少种可能的正确密码,使得每个正确密码 都能够按照他所采用的锁车方式产生锁车后密码锁的全部 n 个状态。
【输入格式】
从文件 lock.in 中读入数据。
输入的第一行包含一个正整数 n,表示锁车后密码锁的状态数。 接下来 n 行每行包含五个整数,表示一个密码锁的状态。
【输出格式】
输出到文件 lock.out 中。
输出一行包含一个整数,表示密码锁的这 n 个状态按照给定的锁车方式能对应多 少种正确密码。
【样例 1 输入】
1
0 0 1 1 5
【样例 1 输出】
81
【样例 1 解释】
一共有 81 种可能的方案。
其中转动一个拨圈的方案有 45 种,转动两个拨圈的方案有 36 种。 【样例 2】
见选手目录下的 lock/lock2.in 与 lock/lock2.ans。 【数据范围】
对于所有测试数据有:1 ≤ n ≤ 8。
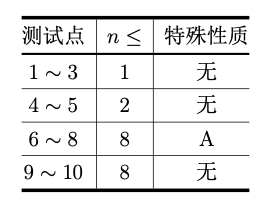
特殊性质 A:保证所有正确密码都可以通过仅转动一个拨圈得到测试数据给出的 n 个状态。