擂台游戏(arena)
【题目描述】
小 S 想要举办一场擂台游戏,如果共有 2k 名选手参加,那么游戏分为 k 轮进行:
第一轮编号为 1, 2 的选手进行一次对局,编号为 3, 4 的选手进行一次对局,以此
类推,编号为 2k − 1, 2k 的选手进行一次对局。
第二轮在只保留第一轮的胜者的前提下,相邻的两位依次进行一场对局。
以此类推,第 k − 1 轮在只保留第 k − 2 轮的 4 位胜者的前提下,前两位、后两位分别进行对局,也就是所谓的半决赛。
第 k 轮即为半决赛两位胜者的决赛。
确定了游戏晋级的规则后,小 S 将比赛的规则设置为了擂台赛。具体而言,每位选 手都有一个能力值 a1 , a2 , · · · , a2k ,能力值为 [0, 231 − 1] 之内的整数。对于每场比赛,会 先抽签决定一个数 0/1,我们将第 R 轮的第 G 场比赛抽到的数记为 dR,G。抽到 0 则表 示表示编号小的选手为擂主,抽到 1 则表示编号大的选手为擂主。擂主获胜当且仅当他 的能力值 a ≥ R。也就是说,游戏的胜负只取决于擂. 主. 的. 能. 力. 值. 与当. 前. 比. 赛. 是. 第. 几. 轮. 的 大小关系,与. 另. 一. 位. 的. 能. 力. 值. 无. 关. 。
现在,小 S 先后陆续收到了 n 位选手的报名信息,他们分别告知了小 S 自己的能 力值。小 S 会按照报名的先后顺序对选手进行编号为 1, 2, · · · , n。小 S 关心的是,补充 尽. 量. 少. 的选手使总人数为 2 的整次幂,且所有选手进行一次完整的擂台游戏后,所有可 能成为总冠军的选手的编. 号. 之. 和. 为多少。
形式化地,设 k 是最小的非负整数使得 2k ≥ n,那么应当补充 (2k − n) 名选手,且 补充的选手的能力值可以任取[0,231−1]之内的整数。如.果.补.充.的.选.手.有.可.能.获.胜.,也. 应. 当. 计. 入. 答. 案. 中. 。
当然小 S 觉得这个问题还是太简单了,所以他给了你 m 个询问 c1, c2, · · · , cm。小 S 希望你帮忙对于每个 ci 求出,在只收到前 ci 位选手的报名信息时,这个问题的答案 是多少。
【输入格式】
从文件 arena.in 中读入数据。
本. 题. 的. 测. 试. 点. 包. 含. 有. 多. 组. 测. 试. 数. 据.,但不同测试数据只是通过修改a1,a2,··· ,an 得 到,其他内容均保持不变,请参考以下格式。其中 ⊕ 代表异或运算符,a mod b 代表 a 除以 b 的余数。
输入的第一行包含两个正整数 n, m,表示报名的选手数量和询问的数量。
输入的第二行包含 n 个非负整数 a′1, a′2, · · · , a′n,这列数将用来计算真正的能力值。
输入的第三行包含 m 个正整数 c1, c2, · · · , cm,表示询问。
设K是使得2K ≥n的最小的非负整数,接下来的K行当中,第R行包含2K−R个数(无空格),其中第 G 个数表示第 R 轮的第 G 场比赛抽签得到的 dR,G = 0/1。
注意,由于询问只是将人数凑齐到 2k ≥ ci,这里的 k ≤ K,因此你未必会用到全部 的输入值。
接下来一行包含一个正整数 T,表示有 T 组测试数据。
接下来共 T 行,每行描述一组数据,包含 4 个非负整数 X0, X1, X2, X3,该组数据 的能力值ai =a′i ⊕Ximod4,其中1≤i≤n。
【输出格式】
输出到文件 arena.out 中。
共输出 T 行,对于每组数据,设 Ai 为第 i(1 ≤ i ≤ m)组询问的答案,你只需要 输出一行包含一个整数,表示 (1 × A1) ⊕ (2 × A2) ⊕ · · · ⊕ (m × Am) 的结果。
【样例 1 输入】
5 5
0 0 0 0 0
5 4 1 2 3
1001
10
1
4
2 1 0 0
1 2 1 0
0 2 3 1
2 2 0 1【样例 1 输出】
5
19
7
1【样例 1 解释】
共有 T = 4 组数据,这里只解释第一组。5 名选手的真实能力值为 [1, 0, 0, 2, 1]。5 组询问分别是对长度为 5, 4, 1, 2, 3 的前缀进行的。
1. 对于长度为 1 的前缀,由于只有 1 号一个人,因此答案为 1。
对于长度为 2 的前缀,由于 2 个人已经是 2 的幂次,因此不需要进行扩充。根据 抽签d1,1 = 1可知2号为擂主,由于a2 < 1,因此1号获胜,答案为1。
对于长度为 3 的前缀,首先 1 号、2 号比赛是 1 号获胜(因为 d1,1 = 1,故 2 号 为擂主,a2 < 1),然后虽然 4 号能力值还不知道,但 3 号、4 号比赛一定是 4 号 获胜(因为 d1,2 = 0,故 3 号为擂主,a3 < 1),而决赛 1 号、4 号谁获胜都有可 能(因为d2,1 = 1,故4号为擂主,如果a4 < 2则1号获胜,a4 ≥ 2则4号获 胜)。综上所述,答案为 1 + 4 = 5。
对于长度为 4 的前缀,我们根据上一条的分析得知,由于 a4 ≥ 2 ,所以决赛获 胜的是4 号。
对于长度为 5 的前缀,可以证明,可能获胜的选手包括 4 号、7 号、8 号,答案 为 19。
因此,该组测试数据的答案为(1×19)⊕(2×4)⊕(3×1)⊕(4×1)⊕(5×5) = 5。
【样例 2】
见选手目录下的 arena/arena2.in 与 arena/arena2.ans。 这组样例满足特殊性质 A。
【样例 3】
见选手目录下的 arena/arena3.in 与 arena/arena3.ans。
这组样例满足特殊性质 B。
【样例 4】
见选手目录下的 arena/arena4.in 与 arena/arena4.ans。
【样例 5】
见选手目录下的 arena/arena5.in 与 arena/arena5.ans。
【数据范围】
对于所有测试数据,保证:2 ≤ n,m ≤ 105,0 ≤ ai,Xj < 231,1 ≤ ci ≤ n,1 ≤ T ≤ 256。
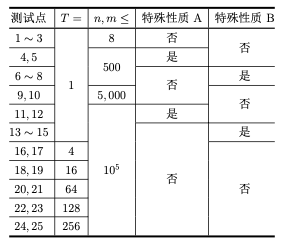
特殊性质 A:保证询问的 ci 均为 2 的幂次。
特殊性质 B:保证所有的 dR,G = 0。