在构建哈夫曼树时 ,每次应该选择( ) 合并。
最⼩权值的节点
最⼤权值的节点
随机节点
深度最深的节点
⾯向对象的编程思想主要包括以下哪些原则 ( ) ?
贪⼼ 、动态规划、 回溯
并发、并⾏ 、异步
递归、循环、分治
封装、继承、多态
在队列中 ,元素的添加和删除是按照( )原则进⾏的。
先进先出
先进后出
最⼩值先出
随机进出
给定⼀个简单的类定义如下,( )语句在类的外部正确地创建了⼀个 Circle 对象并调⽤了 getArea 函数?
1 class Circle {
2 private:
3 double radius;
4 public:
5 Circle(double r) : radius(r) {}
6 double getArea() {
7 return 3.14 * radius * radius;
8 }
9 };
Circle c = Circle(5.0); c.getArea(c);
Circle c(5.0); getArea(c);
Circle c = new Circle(5.0); c.getArea();
Circle c(5.0); c.getArea();
以下代码希望能在⼀棵⼆叉排序树中搜索特定的值 ,请在横线处填⼊( ) ,使其能正确实现相应功能。
1 TreeNode* search(TreeNode* root, int target) {
2 if (root == NULL || root->val == target) {
3 return root;
4 }
5 if (_______________) {
6 return search(root->left, target);
7 } else {
8 return search(root->right, target);
9 }
10 }
target < root->left
target < root->val
target > root->val
target > root->left
3 位格雷编码的正确顺序是( ) 。
000, 001, 010, 011, 100, 101, 110, 111
000, 001, 011, 010, 110, 111, 101, 100
000, 010, 001, 011, 100, 110, 101, 111
000, 010, 110, 100, 111, 101, 011, 001
以下动态规划算法的含义与⽬的是( ) 。
1 int function(vector<int>& nums) {
2 int n = nums.size();
3 if (n == 0)
4 return 0;
5 if (n == 1)
6 return nums[0];
7 vector<int> dp(n, 0);
8 dp[0] = nums[0];
9 dp[1] = max(nums[0], nums[1]);
10 for (int i = 2; i < n; ++i) {
11 dp[i] = max(dp[i - 1], nums[i] + dp[i - 2]);
12 }
13 return dp[n - 1];
14 }
计算数组 nums 中的所有元素的和
计算数组 nums 中相邻元素的最大和
计算数组 nums 中不相邻元素的最大和
计算数组 nums 中的最小元素
阅读以下广度优先搜索的代码:
1 void bfs(TreeNode* root) {
2 if (root == NULL) {
3 return;
4 }
5 queue<TreeNode*> q;
6 q.push(root);
7 while (!q.empty()) {
8 TreeNode* current = q.front();
9 q.pop();
10 cout << current->val << " ";
11 if (current->left) {
12 q.push(current->left);
13 }
14 if (current->right) {
15 q.push(current->right);
16 }
17 }
18 }使用以上算法遍历以下这棵树,可能的输出是( )。

1 2 8 9 4 5 3 6 7 10 11
1 2 3 4 5 6 7 8 9 10 11
1 2 3 8 9 6 4 5 7 10 11
1 2 3 8 9 4 5 6 7 10 11
给定一个空栈,执行以下操作序列:
操作序列:push(1), push(2), push(3), pop( ), pop( ), push(4), push(5), pop( )
最终栈中的元素是( )。
1, 2
1, 4, 5
1, 2, 5
1, 4
⼀个有 124 个叶⼦节点的完全⼆叉树 ,最多有( )个结点。
247
248
249
250
在求解最优化问题时 ,动态规划常常涉及到两个重要性质, 即最优⼦结构和( ) 。
重叠⼦问题
分治法
贪⼼策略
回溯算法
若⼀棵⼆叉树的先序遍历为:A, B, D, E, C, F 、 中序遍历为:D, B, E, A, F, C ,它的后序遍历为( ) 。
D, E, B, F, C, A
E, D, B, F, C, A
D, E, B, C, F, A
E, D, B, C, F, A
线性筛法与埃⽒筛法相⽐的优势是( ) 。
更容易实现
更节省内存
更快速
更准确
以下代码使⽤了辗转相除法求解最⼤公因数 ,请在横线处填⼊( ) ,使其能正确实现相应功能。
1 int gcd(int a, int b) {
2 while (b != 0) {
3 _________________________
4 }
5 return a;
6 }
int temp = b; b = a / b; a = temp;
int temp = a; a = b / a; b = temp;
int temp = b; b = a % b; a = temp;
b = a % b; a = b;
下⾯的代码⽚段⽤于反转单链表 ,请进⾏( ) 修改 ,使其能正确实现相应功能。
1 ListNode* reverseLinked List(ListNode* head) {
2 ListNode* prev = nullptr;
3 ListNode* current = head;
4 while (current != nullptr) {
5 ListNode* next = current->next;
6 current->next = next;
7 prev = current;
8 current = next;
9 }
10 return prev;
11 }
current->next = next; 应该改为 current->next = prev;
ListNode* next = current->next; 应该改为 ListNode* next = prev->next;
current != nullptr 应该改为 current->next != nullptr
ListNode* prev = nullptr; 应该改为 ListNode* prev = head;
哈夫曼树是一种二叉树。( )
继承是将已有类的属性和方法引入新类的过程。( )
完全二叉树的任意一层都可以不满。( )
哈夫曼编码的主要应用领域是有损数据压缩。( )
试题名称:游戏
3.1.1 题面描述
你有四个正整数n,a,b,c ,并准备用它们玩一个简单的小游戏。
在一轮游戏操作中,你可以选择将n减去a,或是将n减去b。游戏将会进行多轮操作,直到当n≤c时游戏结束。
你想知道游戏结束时有多少种不同的游戏操作序列。两种游戏操作序列不同,当且仅当游戏操作轮数不同,或是某一轮游戏操作中,一种操作序列选择将n减去a,而另一种操作序列选择将n减去b。如果a=b,也认为将n减去a与将n减去b是不同的操作。
由于答案可能很⼤,你只需要求出答案对1000000007 取模的结果。
3.1.2 输入格式
一行四个正整数n,a,b,c 。保证1≤a,b,c≤n 。
3.1.3 输出格式
一行一个整数,表示不同的游戏操作序列数量对1000000007取模的结果。
3.1.4 样例1
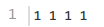
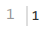
3.1.5 样例2
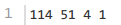
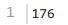
3.1.6 样例3
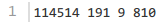

3.1.7 数据范围
对于20的测试点,保证a=b=c=1,n≤30 。
对于40的测试点,保证c=1,n≤103 。
对于所有测试点,保证1≤n≤2×105 。
试题名称:好斗的牛
3.2.1 问题描述
你有 个牛棚,从左到右一字排开。你希望把N头牛安置到牛棚里。麻烦的是,你的牛很好斗,如果他们附近有其他的牛,他们就会不安分地去挑事。其中,第 i头牛的攻击范围是(ai,bi),这意味着,如果他的左边ai个牛棚或右边bi个牛棚里有其他牛,他就会去挑事。
你想留下连续的一段牛棚,并把其他牛棚都卖掉。请问你最少需要留下多少牛棚,才能保证至少存在一种方案能够把所有的N头牛都安置进剩余的牛棚里,且没有牛会挑事?
3.2.2 输入描述
第一行 1 个正整数N 。
接下来一行N个用空格隔开的正整数a1,……,an 。
接下来一行N个用空格隔开的正整数b1,……,bn 。
3.2.3 输出描述
输出一行一个整数,表示你最少需要留下多少牛棚。
3.2.4 特别提醒
在常规程序中,输入、输出时提供提示是好习惯。但在本场考试中,由于系统限定,请不要在输入、输出中附带任何提示信息。
3.2.5 样例输入 1
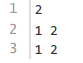
3.2.6 样例输出 1
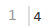
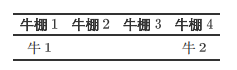
3.2.7 样例解释 1
你可以留下4个牛棚,并如此安排你的牛:
3.2.8 样例输入 2

3.2.9 样例输出 2

3.2.10 数据规模
对于20的测试点,保证N=2 ;
对于另外20的测试点,保证N=3 ;
对于80的测试点,保证N≤8 ;
对于所有测试点,保证N≤9,ai,bi≤1000 。