决斗(duel)

【题目描述】

今天是小 Q 的生日，他得到了 n 张卡牌作为礼物。这些卡牌属于火爆的“决斗怪 兽”，其中，第 i 张卡代表一只攻击力为 ri，防御力也为 ri 的怪兽。

一场游戏分为若干回合。每回合，小 Q 会选择某只怪兽 i 以及另. 一. 只. 怪兽 j(i ̸= j)， 并让怪兽 i 向怪兽 j 发起攻击。此时，若怪兽 i 的攻击力小于等于怪兽 j 的防御力，则 无事发生;否则，怪兽 j 的防御被打破，怪兽 j 退出游戏不再参与到剩下的游戏中。一 只怪兽在整场游戏中至. 多. 只能发起一次攻击。当未退出游戏的怪兽都已发起过攻击时， 游戏结束。

小 Q 希望决定一组攻击顺序，使得在游戏结束时，未退出游戏的怪兽数量尽可能 少。

【输入格式】

从文件 duel.in 中读入数据。
输入的第一行包含一个正整数 n，表示卡牌的个数。
输入的第二行包含 n 个正整数，其中第 i 个正整数表示第 i 个怪兽的攻击力及防御

力 ri。 【输出格式】

输出到文件 duel.out 中。 输出一行包含一个整数表示游戏结束时未退出游戏的怪兽数量的最小值。

【样例 1 输入】 

5
1 2 3 1 2

【样例 1 输出】 

2

【样例 1 解释】

其中一种最优方案为:第一回合让第 2 只怪兽向第 1 只怪兽发起攻击，第二回合 让第 5 只怪兽向第 4 只怪兽发起攻击，第三回合让第 3 只怪兽向第 5 只怪兽发起攻击。 此时没有退出游戏的怪兽都进行过攻击，游戏结束。可以证明没有更优的攻击顺序。

【样例 2 输入】 

 10
136 136 136 2417 136 136 2417 136 136 136

【样例 2 输出】 

8

【样例 3】
见选手目录下的 duel/duel3.in 与 duel/duel3.ans。

该样例满足∀1≤i≤n,ri ≤2。 

【样例 4】

见选手目录下的 duel/duel4.in 与 duel/duel4.ans。

【数据范围】

对于所有测试数据，保证:1 ≤ n ≤ 105，1 ≤ ri ≤ 105。

特殊性质 A:保证每个 ri 在可能的值域中独立均匀随机生成。

超速检测(detect)

【题目描述】

小 D 新入职了某国的交管部门，他的第一个任务是负责国家的一条长度为 L 的南 北主干道的车辆超速检测。为了考考小 D，上司首先需要他解决一个简化的场景。

这个周末，主干道上预计出现 n 辆车，其中第 i 辆车从主干道上距离最南端 di 的 位置驶入，以 vi 的初速度和 ai 的加速度做匀加速运动向北行驶。我们只考虑从南向北 的车辆，故 vi > 0，但 ai 可正可负，也可以为零。当车辆行驶到主干道最北端(即距离 最南端为 L 的位置)或速度降为 0(这只可能在 ai < 0 时发生)时，我们认为该车驶离 主干道。

主干道上设置了 m 个测速仪，其中第 j 个测速仪位于主干道上距离最南端 pj 的位 置，每个测速仪可以设置开启或关闭。当某辆车经过某个开启的测速仪时，若这辆车的 瞬时速度超. 过. 了道路限速 V ，那么这辆车就会被判定为超速。注意当车辆驶入与驶出主 干道时，如果在对应位置有一个开启的测速仪，这个测速仪也会对这辆车进行测速。

上司首先想知道，如果所有测速仪都是开启的，那么这 n 辆车中会有多少辆车被判 定为超速。

其次，为了节能，部门想关闭一部分测速仪。然而，他们不希望漏掉超速的车，也 就是说，当 n 辆车里的某辆车在所有测速仪都开启时被判定为超速，他们希望在关闭一 部分测速仪以后它依然被判定为超速。上司还想知道在这样的条件下最多可以关闭多少 测速仪。

由于 n 很大，上司允许小 D 使用编程解决这两个问题，于是小 D 找到了你。

如果你对于加速度并不熟悉，小 D 贴心地在本题的“提示”部分提供了有关加速 度的公式。

【输入格式】

从文件 detect.in 中读入数据。
本. 题. 有. 多.组.测.试. 数. 据.。
输入的第一行包含一个正整数 T，表示数据组数。
接下来包含 T 组数据，每组数据的格式如下:
第一行包含四个整数 n, m, L, V ，分别表示车辆数量、测速仪数量、主干道长度和

道路限速。 接下来 n 行:

第 i 行包含三个整数 di, vi, ai 描述一辆车。
最后一行包含 m 个整数 p1, p2, · · · , pm 描述道路上所有测速仪的位置。

【输出格式】

输出到文件 detect.out 中。

 对于每组数据:输出一行包含两个整数，第一个整数为所有测速仪都开启时被判定为超速的车辆数量，第二个整数为在不漏掉超速车辆的前提下最多可以关闭的测速仪数量。

【样例 1 输入】

1
5 5 15 3
0 3 0
12 4 0
1 1 4
5 5 ‐2
6 4 ‐4
2 5 8 9 15

【样例 1 输出】 

3 3

【样例 1 解释】

在该组测试数据中，主干道长度为 15，限速为 3，在距离最南端 2, 5, 8, 9, 15 的位置 各设有一个测速仪。

• 第一辆车在最南端驶入，以 3 的速度匀速行驶。这辆车在整个路段上都没有超速。

• 第二辆车在距离最南端 12 的位置驶入，以 4 的速度匀速行驶。在最北端驶离主

  干道时，它会被距离最南端 15 的测速仪判定为超速。

• 第三辆车在距离最南端 1 的位置驶入，以 1 的初速度、4 的加速度行驶。其在行驶了 32 −12 = 1 的距离，即到达 2 的位置时，速度变为 3，并在之后一直超速。因 2×4

• 此这辆车会被除了距离最南端 2 的测速仪以外的其他测速仪判定为超速。

• 第四辆车在距离最南端 5 的位置驶入，以 5 的初速度、−2 的加速度行驶。其在行驶了 32−52 = 4 的距离，即到达 9 的位置时，速度变为 3。因此这辆车在距离 2×(−2)

• 最南端 [5, 9) 时超速，会被距离最南端 5 和 8 的两个测速仪判定为超速。

• 第五辆车在距离最南端 6 的位置驶入，以 4 的初速度、−4 的加速度行驶。在其 行驶了 32−42 = 7 的距离后，即这辆车到达 67 的位置时，其速度变为 3。因此这辆车在距离最南端 [6, 6 87 ) 时超速，但这段区间内没有测速仪，因此不会被判定为超速。

因此第二、三、四辆车会被判定为超速，输出的第一个数为 3。 我们可以关闭距离最南端 2, 8, 9 的三个测速仪，保留 5 和 15 的两个测速仪，此时

三辆之前被判定为超速的车依然被判定为超速。可以证明不存在更优方案，因此输出的 第二个数为 3。

【样例 2】
见选手目录下的 detect/detect2.in 与 detect/detect2.ans。

该组样例满足 n, m ≤ 10。 

【样例 3】

见选手目录下的 detect/detect3.in 与 detect/detect3.ans。 该组样例满足特殊性质 A，其中前十组测试数据满足 n, m ≤ 3000。

【样例 4】
见选手目录下的 detect/detect4.in 与 detect/detect4.ans。

该组样例满足特殊性质 B，其中前十组测试数据满足 n, m ≤ 3000。 

【样例 5】

见选手目录下的 detect/detect5.in 与 detect/detect5.ans。 该组样例满足特殊性质 C，其中前十组测试数据满足 n, m ≤ 3000。

【数据范围】

对于所有测试数据，保证:
• 1 ≤ T ≤ 20;
• 1≤n,m≤105，1≤L≤106，1≤V ≤103; • 0≤di <L，1≤vi ≤103，|ai|≤103;
• 0≤p1 <p2 <···<pm ≤L。

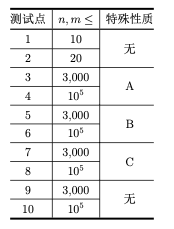
特殊性质 A:保证 ai = 0。
特殊性质 B:保证 ai > 0。
特殊性质 C:保证 ai < 0，且所有车都不在最北端驶离主干道。

【提示】

与加速度有关的定义和公式如下:
• 匀加速运动 是指物体在运动过程中，加速度保持不变的运动，即每单位时间内

速度的变化量是恒定的。
• 当一辆车的初速度为 v0、加速度 a ̸= 0，做匀加速运动，则 t 时刻后它的速度

v1 = v0 +a×t，它的位移(即行驶路程)s = v0 ×t+0.5×a×t2。
• 当一辆车的初速度为 v0、加速度 a ̸= 0，做匀加速运动，则当它的位移(即行驶路程)为 s 时，这辆车的瞬时速度为 √v02 + 2 × a × s。

•当一辆车的初速度为v0、加速度a̸=0，在它的位移(即行驶路程)为v12−v02 时， 2a这辆车的瞬时速度为 v1。 

如果你使用浮点数进行计算，需要注意潜在的精度问题。

染色(color)

【题目描述】

给定一个长度为 n 的正整数数组 A，其中所有数从左至右排成一排。 你需要将 A 中的每个数染成红色或蓝色之一，然后按如下方式计算最终得分: 设 C 为长度为 n 的整数数组，对于 A 中的每个数 Ai(1 ≤ i ≤ n):

• 如果 Ai 左侧没有与其同色的数，则令 Ci = 0。 •否则，记其左侧与.其.最.靠.近.的.同.色.数.为Aj，若Ai =Aj，则令Ci =Ai，否则令Ci = 0。

你的最终得分为 C 中所有整数的和，即你需要最大化最终得分，请求出最即终得分的最大值。

【输入格式】

从文件 color.in 中读入数据。

本. 题. 有. 多.组.测.试. 数. 据.。
输入的第一行包含一个正整数 T，表示数据组数。
接下来包含 T 组数据，每组数据的格式如下: 第一行包含一个正整数 n，表示数组长度。
第二行包含 n 个正整数 A1, A2, . . . , An，表示数组 A 中的元素。

【输出格式】

输出到文件 color.out 中。 对于每组数据:输出一行包含一个非负整数，表示最终得分的最大可能值。

【样例 1 输入】

3
3
1 2 1
4
1 2 3 4
8
3 5 2 5 1 2 1 4

【样例 1 输出】

1 
0 
8

【样例 1 解释】

对于第一组数据，以下为三种可能的染色方案:
1. 将 A1, A2 染成红色，将 A3 染成蓝色(121)，其得分计算方式如下:

• 对于 A1，由于其左侧没有红色的数，所以 C1 = 0。

• 对于 A2，其左侧与其最靠近的红色数为 A1。由于 A1 ̸= A2，所以 C2 = 0。

• 对于 A3，由于其左侧没有蓝色的数，所以 C3 = 0。

  该方案最终得分为C1 +C2 +C3 = 0。

2. 将 A1, A2, A3 全部染成红色(121)，其得分计算方式如下:

• 对于 A1，由于其左侧没有红色的数，所以 C1 = 0。

• 对于 A2，其左侧与其最靠近的红色数为 A1。由于 A1 ̸= A2，所以 C2 = 0。

• 对于 A3，其左侧与其最靠近的红色数为 A2。由于 A2 ̸= A3，所以 C3 = 0。

  该方案最终得分为C1 +C2 +C3 = 0。

3. 将 A1, A3 染成红色，将 A2 染成蓝色(121)，其得分计算方式如下:

• 对于 A1，由于其左侧没有红色的数，所以 C1 = 0。

• 对于 A2，由于其左侧没有蓝色的数，所以 C2 = 0。

• 对于 A3，其左侧与其最靠近的红色数为 A1。由于 A1 = A3，所以 C3 = A3 = 1。

  该方案最终得分为C1 +C2 +C3 = 1。 可以证明，没有染色方案使得最终得分大于 1。 对于第二组数据，可以证明，任何染色方案的最终得分都是 0。 对于第三组数据，一种最优的染色方案为将 A1, A2, A4, A5, A7 染为红色，将 A3, A6, A8

  染为蓝色(35152124)，其对应 C = [0, 0, 0, 5, 0, 1, 2, 0]，最终得分为 8。 

【样例 2】

见选手目录下的 color/color2.in 与 color/color2.ans。 

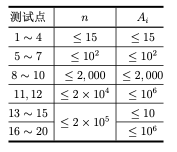
【数据范围】

对于所有测试数据，保证:1 ≤ T ≤ 10，2 ≤ n ≤ 2×105，1 ≤ Ai ≤ 106。

擂台游戏(arena)

【题目描述】

小 S 想要举办一场擂台游戏，如果共有 2k 名选手参加，那么游戏分为 k 轮进行:

• 第一轮编号为 1, 2 的选手进行一次对局，编号为 3, 4 的选手进行一次对局，以此

  类推，编号为 2k − 1, 2k 的选手进行一次对局。

• 第二轮在只保留第一轮的胜者的前提下，相邻的两位依次进行一场对局。

• 以此类推，第 k − 1 轮在只保留第 k − 2 轮的 4 位胜者的前提下，前两位、后两位分别进行对局,也就是所谓的半决赛。

第 k 轮即为半决赛两位胜者的决赛。

确定了游戏晋级的规则后，小 S 将比赛的规则设置为了擂台赛。具体而言，每位选 手都有一个能力值 a1 , a2 , · · · , a2k ，能力值为 [0, 231 − 1] 之内的整数。对于每场比赛，会 先抽签决定一个数 0/1，我们将第 R 轮的第 G 场比赛抽到的数记为 dR,G。抽到 0 则表 示表示编号小的选手为擂主，抽到 1 则表示编号大的选手为擂主。擂主获胜当且仅当他 的能力值 a ≥ R。也就是说，游戏的胜负只取决于擂. 主. 的. 能. 力. 值. 与当. 前. 比. 赛. 是. 第. 几. 轮. 的 大小关系，与. 另. 一. 位. 的. 能. 力. 值. 无. 关. 。

现在，小 S 先后陆续收到了 n 位选手的报名信息，他们分别告知了小 S 自己的能 力值。小 S 会按照报名的先后顺序对选手进行编号为 1, 2, · · · , n。小 S 关心的是，补充 尽. 量. 少. 的选手使总人数为 2 的整次幂，且所有选手进行一次完整的擂台游戏后，所有可 能成为总冠军的选手的编. 号. 之. 和. 为多少。

形式化地，设 k 是最小的非负整数使得 2k ≥ n，那么应当补充 (2k − n) 名选手，且 补充的选手的能力值可以任取[0,231−1]之内的整数。如.果.补.充.的.选.手.有.可.能.获.胜.，也. 应. 当. 计. 入. 答. 案. 中. 。

当然小 S 觉得这个问题还是太简单了，所以他给了你 m 个询问 c1, c2, · · · , cm。小 S 希望你帮忙对于每个 ci 求出，在只收到前 ci 位选手的报名信息时，这个问题的答案 是多少。

【输入格式】

从文件 arena.in 中读入数据。

本. 题. 的. 测. 试. 点. 包. 含. 有. 多. 组. 测. 试. 数. 据.，但不同测试数据只是通过修改a1,a2,··· ,an 得 到，其他内容均保持不变，请参考以下格式。其中 ⊕ 代表异或运算符，a mod b 代表 a 除以 b 的余数。

输入的第一行包含两个正整数 n, m，表示报名的选手数量和询问的数量。

输入的第二行包含 n 个非负整数 a′1, a′2, · · · , a′n，这列数将用来计算真正的能力值。 

输入的第三行包含 m 个正整数 c1, c2, · · · , cm，表示询问。

设K是使得2K ≥n的最小的非负整数，接下来的K行当中，第R行包含2K−R个数(无空格)，其中第 G 个数表示第 R 轮的第 G 场比赛抽签得到的 dR,G = 0/1。

注意，由于询问只是将人数凑齐到 2k ≥ ci，这里的 k ≤ K，因此你未必会用到全部 的输入值。

接下来一行包含一个正整数 T，表示有 T 组测试数据。

接下来共 T 行，每行描述一组数据，包含 4 个非负整数 X0, X1, X2, X3，该组数据 的能力值ai =a′i ⊕Ximod4，其中1≤i≤n。

【输出格式】

输出到文件 arena.out 中。

共输出 T 行，对于每组数据，设 Ai 为第 i(1 ≤ i ≤ m)组询问的答案，你只需要 输出一行包含一个整数，表示 (1 × A1) ⊕ (2 × A2) ⊕ · · · ⊕ (m × Am) 的结果。

【样例 1 输入】

5 5
0 0 0 0 0
5 4 1 2 3
1001
10
1
4
2 1 0 0
1 2 1 0
0 2 3 1
2 2 0 1

【样例 1 输出】

5 
19 
7 
1

【样例 1 解释】

共有 T = 4 组数据，这里只解释第一组。5 名选手的真实能力值为 [1, 0, 0, 2, 1]。5 组询问分别是对长度为 5, 4, 1, 2, 3 的前缀进行的。

1. 对于长度为 1 的前缀，由于只有 1 号一个人，因此答案为 1。

2. 对于长度为 2 的前缀，由于 2 个人已经是 2 的幂次，因此不需要进行扩充。根据 抽签d1,1 = 1可知2号为擂主，由于a2 < 1，因此1号获胜，答案为1。

3. 对于长度为 3 的前缀，首先 1 号、2 号比赛是 1 号获胜(因为 d1,1 = 1，故 2 号 为擂主，a2 < 1)，然后虽然 4 号能力值还不知道，但 3 号、4 号比赛一定是 4 号 获胜(因为 d1,2 = 0，故 3 号为擂主，a3 < 1)，而决赛 1 号、4 号谁获胜都有可 能(因为d2,1 = 1，故4号为擂主，如果a4 < 2则1号获胜，a4 ≥ 2则4号获 胜)。综上所述，答案为 1 + 4 = 5。

4. 对于长度为 4 的前缀，我们根据上一条的分析得知，由于 a4 ≥ 2 ，所以决赛获 胜的是4 号。

5. 对于长度为 5 的前缀，可以证明，可能获胜的选手包括 4 号、7 号、8 号，答案 为 19。

因此，该组测试数据的答案为(1×19)⊕(2×4)⊕(3×1)⊕(4×1)⊕(5×5) = 5。 

【样例 2】

见选手目录下的 arena/arena2.in 与 arena/arena2.ans。 这组样例满足特殊性质 A。

【样例 3】
见选手目录下的 arena/arena3.in 与 arena/arena3.ans。

这组样例满足特殊性质 B。 

【样例 4】

见选手目录下的 arena/arena4.in 与 arena/arena4.ans。 

【样例 5】

见选手目录下的 arena/arena5.in 与 arena/arena5.ans。 

【数据范围】

对于所有测试数据，保证:2 ≤ n,m ≤ 105，0 ≤ ai,Xj < 231，1 ≤ ci ≤ n，1 ≤ T ≤ 256。

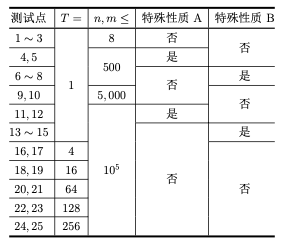
特殊性质 A:保证询问的 ci 均为 2 的幂次。

特殊性质 B:保证所有的 dR,G = 0。