2023年9月CCF GESP编程能力认证C++等级考试（五级）试卷

单选题

第 1 题单选题

近年来，线上授课变得普遍，很多有助于改善教学效果的设备也逐渐流行，其中包括比较常用的手写板，那么它属于哪类设备?( )。

输入

输出

控制

记录

第 2 题单选题

归并排序算法的基本思想是（）。

将数组分成两个子数组，分别排序后再合并。

随机选择一个元素作为枢轴，将数组划分为两个部分。

从数组的最后一个元素开始，依次与前一个元素比较并交换位置。

比较相邻的两个元素，如果顺序错误就交换位置。

第 3 题单选题

在上题的归并排序算法中， mergeSort(listData, start, middle); 和 mergeSort(listData, middle + 1, end); 涉及到的算法为（）。

搜索算法

分治算法

贪心算法

递推算法

第 4 题单选题

下面代码用于归并排序，其中 merge() 函数被调用次数为（）。

第 5 题单选题

下面代码中的 isPrimeA() 和 isPrimeB() 都用于判断参数 N 是否素数，有关其时间复杂度的正确说法是（）。

isPrimeA() 的最坏时间复杂度是， isPrimeB() 的最坏时间复杂度是， isPrimeB() 优于 isPrimeA() 。

isPrimeA() 的最坏时间复杂度是， isPrimeB() 的最坏时间复杂度是， isPrimeA() 优于 isPrimeB() 。

isPrimeA() 的最坏时间复杂度是， isPrimeB() 的最坏时间复杂度是， isPrimeA() 优于 isPrimeB()

第 6 题单选题

下面代码执行后的输出是（）

4#3#2#2#4

4#3#2#2#1#5

4#3#2#1#2#4

4#3#2#1#2#5

第 7 题单选题

有关下面C++代码正确的是（）。

checkNum() 函数定义错误。

输出行 A 的语句将导致编译错误。

输出行 B 的语句将导致编译错误。

该代码没有编译错误。

第 8 题单选题

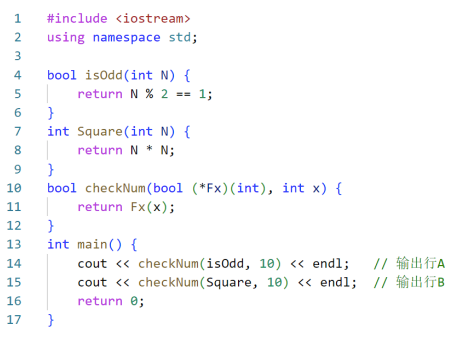
有关下面代码正确的是（）。

checkNum() 函数定义错误。

将 isEven 作为 checkNum() 参数将导致错误。

执行后将输出 1 。

运行时触发异常。

第 9 题单选题

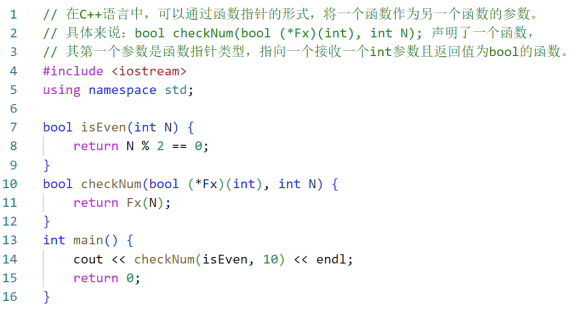
根据下面C++代码的注释，两个横线处应分别填入（）

compare 和 isOdd(lstA[i])

compare(x1,y1) 和 isOdd

compare 和 isOdd

compare(x1,y1) 和 isOdd(lstA[i])

第 10 题单选题

印度古老的汉诺塔传说:创世时有三根金刚柱，其中一柱从下往上按照大小顺序摞着64片黄金圆盘，当圆盘逐一从一柱借助另外一柱全部移动到另外一柱时，宇宙毁灭。移动规则:在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。下面的C++代码以递归方式实现汉诺塔，横线处应填入代码是( )。

Hanoi(B, C, A, N - 2)

Hanoi(B, A, C, N - 1)

Hanoi(A, B, C, N - 2)

Hanoi(C, B, A, N - 1)

第 11 题单选题

下面C++代码以递归方式实现字符串反序，横线处应填上代码是( )。

sIn[sIn.length() - 1] + sReverse(sIn.substr(0, sIn.length() - 1));

sIn[0] + sReverse(sIn.substr(1, sIn.length() - 1));

sReverse(sIn.substr(0, sIn.length() - 1)) + sIn[sIn.length() - 1];

sReverse(sIn.substr(1, sIn.length() - 1)) + sIn[sIn.length() - 1];

第 12 题单选题

有关下面C++代码说法错误的是( )。

sumA() 用循环方式求从 1 到 N 之和， sumB() 用递归方式求从 1 到 N 之和。

默认情况下，如果输入正整数 1000 ，能实现求从 1 到 1000 之和。

默认情况下，如果输入正整数 100000 ，能实现求从 1 到 100000 之和。

一般说来， sumA() 的效率高于 sumB() 。

第 13 题单选题

如果变量 a 和 b 分别为 double 类型和 int 类型，则表达式 (a = 6, b = 3 * (7 + 8) / 2, b += a) 的计算结果为（）。

不确定

第 14 题单选题

如果 a 和 b 均为 int 类型的变量，且 b 的值不为 0 ，那么下列能正确判断“ a 是 b 的3倍”的表达式是（）。

(a >> 3 == b)

(a - b) % 3 == 0

(a / b == 3)

(a == 3 * b)

第 15 题单选题

有关下面代码的说法正确的是（）。

上述代码构成单向链表。

上述代码构成双向链表。

上述代码构成循环链表。

上述代码构成指针链表。

判断题

第 16 题判断题

TCP/IP的传输层的两个不同的协议分别是UDP和TCP。

正确

错误

第 17 题判断题

质数的判定和筛法的目的并不相同，质数判定旨在判断特定的正整数是否为质数，而质数筛法意在筛选出范围内的所有质数。

正确

错误

第 18 题判断题

C++语言中的 qsort 库函数是不稳定排序。

正确

错误

第 19 题判断题

一般说来，冒泡排序算法优于归并排序。

正确

错误

第 20 题判断题

贪心算法的解可能不是最优解。

正确

错误

第 21 题判断题

在C++中，通过恰当的实现，可以将链表首尾相接，形成循环链表。

正确

错误

第 22 题判断题

在C++中，可以使用二分法查找链表中的元素。

正确

错误

第 23 题判断题

找出自然数 N 以内的所有质数，常用算法有埃氏筛法和线性筛法，其中埃氏筛法效率更高。

正确

错误

第 24 题判断题

在特殊情况下流程图中可以出现三角框和圆形框。

正确

错误

第 25 题判断题

下面的C++代码执行后将输出 0 5 1 6 2 3 4 。

正确

错误

编程题

第 26 题问答题

试题名称：因数分解

时间限制：1.0 s

内存限制：128.0 MB

【问题描述】

每个正整数都可以分解成素数的乘积，例如：6=2×3、20=22×5，现在，给定一个正整数N，请按要求输出它的因数分解式。

【输入描述】

输入第一行，包含一个正整数N。约定2≤N≤1012

【输出描述】

输出一行，为N的因数分解式。要求按质因数由小到大排列，乘号用星号*表示，且左右各空一格。当且仅当一个素数出现多次时，将它们合并为指数形式，用上箭头^表示，且左右不空格。

样例输入1

样例输出1

2 * 3

样例输入2

样例输出2

2^2 * 5

样例输入3

样例输出3

查看答案

第 27 题问答题

试题名称：巧夺大奖

时间限制：1.0 s

内存限制：128.0 MB

【问题描述】

小明参加了一个巧夺大奖的游戏节目。主持人宣布了游戏规则：

1、游戏分为n个时间段，参加者每个时间段可以选择一个小游戏。

2、游戏中共有n个小游戏可供选择。

3、每个小游戏有规定的时限和奖励。对于第i个小游戏，参加者必须在第Ti个时间段结束前完成才能得到奖励Ri。

小明发现，这些小游戏都很简单，不管选择哪个小游戏，他都能在一个时间段内完成。关键问题在于，如何安排每个时间段分别选择哪个小游戏，才能使得总奖励最高？

【输入描述】

输入第一行，包含一个正整数n。既是游戏时间段的个数，也是小游戏的个数。约定1≤n≤500。

输入第二行，包含n个正整数。第i个正整数为Ti，即第i个小游戏的完成期限。约定1≤Ti≤n。

输入第三行，包含n个正整数。第i个正整数为Ri，即第i个小游戏的完成奖励。约定1≤Ri≤1000。

【输出描述】

输出一行，包含一个正整数C，为最高可获得的奖励。

样例输入1

4 2 4 3 1 4 6

70 60 50 40 30 20 10

样例输出1

230

样例解释1

7个时间段可分别安排完成第4、2、3、1、6、7、5个小游戏，其中第4、2、3、1、7个小游戏在期限内完成。因此，可以获得总计40+60+50+70+10=230的奖励。

查看答案

答题卡

单选题

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

判断题

16 17 18 19 20 21 22 23 24 25

编程题

26 27