自1946年ENIAC计算机问世, 计算机的发展经历了四个时代, 第二个时代计算机的特征是( )。
电子管计算机
小规模集成电路计算机
晶体管计算机
大规模集成电路计算机
对于递归,以下说法错误的是()。
递归适合解决数据的定义是按递归定义的问题
递归算法用递归函数来实现,可以直接或者间接地调用函数自身
递归函数不需要终止条件,可以无限调用自身
递归函数需要调用栈,注意防止栈溢出。
下列( ) 算法的时间复杂度为 o(nlogn)。
选择排序
归并排序
冒泡排序
插入排序
在一篇文章中,字母“a”、“b”、“c”、“d”出现的次数分别为 700、600、300、200,要通过二进制哈夫曼编码对它们进行压缩,那么,字母“d”的编码长度是()。
1
2
3
5
原字符串中任意一段连续的字符组成的新字符串称为子串。则字符串“AABCABC”共有( ) 个不同的非空子串。
20
21
22
23
有向图G入度是2023,则出度是( )。
0
2023
2022
2024
对一个n个顶点、m条边的带权有向简单图,用 Diikstra 算法计算单源最短路时,如果使用二叉堆进行优化,则其时间复杂度为( )。
O(mn + n3)
o(n2)
o((m + n2) log n)
O((m + n) log n)
在 C++中,设 x=12,y=20,则以下表达式值为真的是( )。
(-12+20>x)&&(y>0)
(x<0)1I(!(y>0))
(x>y)ll(y>0)
x>=y&&y>10
如图所示数据库中的一行称为( )。
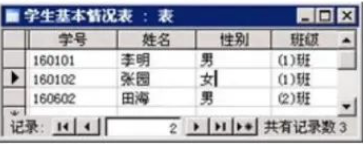
一个数据库
一个字段
一条记录
一个数据表
把 8个同样的球放在 5个同样的袋子里,允许有的袋子空着不放,问共有 ( ) 个不同的分法。(提示:如果8个球都放在一个袋子里,无论是哪个袋子,都只算同一种分法)
22
24
18
20
数组 a和数组 b 的数据存放情况如下表,则 a[a[b[4]+1]]的值是 ( )。

2
3
5
4
在 C++中,若n=3,下面程序段执行后,变量 s 的值是( )。
int s=0;
for(int i=1;i<=n;i++) {
for(int j=1;j<=i;j++) {
if(i%j==0) s++;
}
}4
5
6
7
运行下列程序时,则程序的输出结果是()。
#include<bits/stdc++.h>
using namespace std;
int main ()
{
string s,t;
s="abcababc";
t=s. substr(3,3);
cout<<t;
return 0:
}
abc
bca
cab
aba
在 C++中,若m=5,n=2,下面程序段执行后,变量t的值是( )。
int m,n,t=0;
while(m>0){
m=m-n;
t++;
}
0
1
2
3
当a=3,b=6,c=7 时,表达式axb? ((axc) ?a: c):((b>c) ?: c) 的值是( )。
3
6
7
0
在 C++中,下面程序段执行后,输出结果是(
int a=1,b=2,c;
printf("%d+%d=%d"a,b,a+b);
a b c
a+b a+b
1 2 3
1+2 3
已知一个栈的入栈序列是 a,c,e,h,r,t,e,其出栈序列可能的是 ( )。
c, h, e, a, t, e, r
h, e, c, t, a, r, e
t, e, a, c, h, e, r
r, e, t, e, a, c, h
在 C++中,表达式 abs(2-3)的值是( )。
-1
0
1
2
如图,在某城市中M、N两地之间有整齐的方格形道路网,甲要沿着道路从M处到达N处,要求选择一条最短路径的走,甲总共有( )种走法。
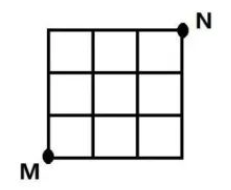
12
18
20
24
在C++中,若x的数据类型为整型且值为9,表达式x/2的值是( )。
1
4
3
4.5
变量a=7,b=9,执行语句a+=a+b后,变量a的值为()。
23
16
7
9
已知问题是“求1000以内能被11整除的整数个数”,解决该问题最合适的算法是( )。
枚举法
贪心法
动态规划
二分查找法
下面四个数中,值与其他三个不同的是()。
(01010110)2
126)8
(54)16
(86)10
下列选项中,属于计算机系统软件的是( )。
IE浏览器
键盘
Linux
显示器
在C++中, char型数据通常占的字节数是( )。
1
2
3
4
算法的三种基本结构分别是顺序结构、选择结构和( )。
分支结构
循环结构
树型结构
重复结构
用一个字节表示整数,则12和-12在计算机内部分别表示为( )。
0000110011110100
0000101111110101
1111010111110100
0000101111110110
在C++中,下列选项可以用作变量名的是( )。
char
1a
a1
%a
下列关于计算机语言的说法中,不正确的是( )。
机器语言是计算机唯一能直接识别并执行的语言
与汇编语言相比,高级语言程序更容易阅读
高级语言比机器语言更高级,是因为它的程序运行效率更高
高级语言程序比汇编语言程序更容易从一种计算机移植到另一种计算机上
一棵二叉树,其先序遍历的结果是 ABDCE。中序历的结果是 BDAEC,其后序遍历的结果为 ( )。
DBCEA
BBDAEC
CDBECA
ABCDE
可以通过配置 IP 地址 192.168.19.266 使计算机接入网络。
设集合A={1,3,5,8},B={1,5,9},C={5,8},则AN(BUC)={1,5}。
对同一个图而言,拓扑排序的结构是唯一的。
80Mbps 的网络上传速度,理论上1秒可以上传 8MB 数据。
C++语言中,char(65)的结果为 a'。
C++中,a=/b 等价于 a=a/b。
C++中,函数 swap(a,b)是交换a和b的地址。
C++中,变量和常量的值都不可以通过赋值语句改变。
C++中,表达式 2023 % 109 的值是 23%。
递推在算法中的优点是可以减少栈空间的使用。
2023年广西中小学生程序设计挑战赛初赛(进阶组)阅读程序题1:

数组a 最大的数组下标是()。
100
1000
10000
199004
maxn 初始化的值是()。
0
100005
maxint
0x7f
函数 check()的返回值是()类型。
string
boo1
char
int
程序段 26行 31行用到的是()算法。
搜索
排序
二分答案
递推
输入如下两行数据,运行程序输出结果为()。
75 199 499 399 199 599 191 499
100
400
500
101
2023年广西中小学生程序设计挑战赛初赛(进阶组)阅读程序题2:

pd()函数的作用是 ()。
判断所传入的参数是否为质数
判断所传入的参数是否为完全平方数
判断所传入的参数是否为偶数
统计质数的个数
库函数 sgrt() 的头文件名是 ()。
cstdio
iostream
algorithm
cmath
void 代表()类型。
char
int
空类型
float
程序使用的算法是 ()。
贪心
广度优先搜索
深度优先搜索
动态规划
输入如下两行数据,输出结果是( )。
53
1 3 9 2 5
2
5
10
4
动物园里的动物房间一个紧挨着另一个排成一行,房间的门也是一个紧靠着一个,门的宽度都是一样的。有些房间里住着一个动物,有些没有。暴风雨把动物园的门都吹飞了。管理员现在的紧急任务是赶紧找些木板来坚立在那些住着动物的房间面前,防止他们溜出来。最直接的方式可以拿一块长长的木板直接横跨竖立在第一个房间到最后一个房间之间,但是这样太浪费木材长度了,因为有些房间没有动物在里面,可以不竖立木板在这些房间面前。木板供应商可以提供任意长度的木板,但是木板的块数是有限的,而且价格是按照所买的木板总长度计算的,不是按块数计算。管理员想买最小总长度的木板,把任务完成。(提示:例如长度为 3 的木板可以竖立在 3 个紧挨着的房间面前。)
给出 m(1<=m<=59)表示供应商能够提供的木板块数、s(1<=s<=209)表示房间总数、动物的总数n(1<=n<=s),以及每个动物所在房间编号(编号在1到s 之间,请算出拦住所有有动物的房间所需木板的最小总长度。输入: 第一行三个整 m,s,n,意义如题目描述。第二行输入n 个整数,表示动物所在的房间编号,编号并不一定按照从小到大。
输出:一行,一个整数,表示所需木板的最小总长度。
程序如下:

1处应该填 ( )。
return x!=y
return x>y
return x==y
x<y
2处应该填 ( )。
a+1,a+n+1
a,a+n+1
a+1,a+n+1,cmp
a,a+n,cmp
3处应该填 ( )。
a[i]-a[i-1]+1
a[i]-a[i-1]
a[i+1]-a[i]
a[i+1]-a[i]-1
4处应该填 ( )。
a[n]-a[1]
a[n]-a[1]+1
a[n]-a[1]-1
b[n-1]-b[1]
5处应该填 ( )。
i<=n-1
i<=m
i<=m-18&i<=n-1
i<=m-1|li<=n-1
有n个城市,编号为 1,2,3,... ,n。城市之间有 m条双向的公路,每条公路连接着两个城市。从公路一端的城市走到另一端的城市,会损失力气。每次经过一个城市,都会被收取一定的过路费(包括起点和终点)。路上并没有收费站。小明从城市1出发,最终要到达地市n停下,而他的力气最多为 s,出发时他的力气是满的。如果他到达目的地,所剩力气值变成负数了,则他就无法到达城市 n,在旅途中力气是不会恢复的。小明不希望花很多钱,他想知道,在可以到达城市 n 的情况下,他所经过的所有城市中最多的一次收取的费用的最小值是多少。如果他无法到达城市 n,输出 NO。输入格式
第一行3个正整数n,m,s,表示有 n(n<=10099)个城市,mm<=50009)条公路,小明满额力气为 s(s<=le9)。
第二行 n个正整数,分别表示城市 1到城市 n 需要交的费用。再接下来有m行,每行3个正整数x,y(1=x,y<n),z(<=1000)。表示城市x和城市y之间有一条路,从x到y或者从y到x 都需要花费 z 的力气。可能有边连接着相同的城市。输出格式
输出一行,一个整数,表示小明能够到达城市 n 时交费最多的一次的最小值;如果他无法到达城市n,则输出NO
程序如下。


1处应该填( )。
b[tnt].Next=head[x]
b[tnt]. Next=x
b[++tnt]. Next=head[x]
b[tnt]. Next=head[y]
2处应该填( )。
dis[y]>dis[x]+z
dis[y]==dis[x]+z
dis[y]>=dis[x]+z 8& f[y]<money
dis[y]>dis[x]+z 8& f[y]<=money
3处应该填( )。
return dis[n]>s
return dis[n]<=s
return dis[n]<s
return dis[n]==s
4处应该填( )。
spfa(left)
spfa(right)
!spfa(right)
!spfa((left+right)/2)
5处应该填( )。
left
left+1
right
right-1