小苹果(apple)
【题目描述】
小苹果(apple)
小 Y 的桌子上放着 n 个苹果从左到右排成一列,编号为从 1 到 n。
小苞是小 Y 的好朋友,每天她都会从中拿走一些苹果。 每天在拿的时候,小苞都是从左侧第 1 个苹果开始、每隔 2 个苹果拿走 1 个苹果。
随后小苞会将剩下的苹果按原先的顺序重新排成一列。 小苞想知道,多少天能拿完所有的苹果,而编号为 n 的苹果是在第几天被拿走的?
【输入格式】
从文件 apple.in 中读入数据。 输入的第一行包含一个正整数 n,表示苹果的总数。
【输出格式】
输出到文件 apple.out 中。
输出一行包含两个正整数,两个整数之间由一个空格隔开,分别表示小苞拿走所有 苹果所需的天数以及拿走编号为 n 的苹果是在第几天。
【样例 1 输入】
8
【样例 1 输出】
5 5
【样例 1 解释】
小苞的桌上一共放了 8 个苹果。 小苞第一天拿走了编号为 1、4、7 的苹果。 小苞第二天拿走了编号为 2、6 的苹果。 小苞第三天拿走了编号为 3 的苹果。 小苞第四天拿走了编号为 5 的苹果。 小苞第五天拿走了编号为 8 的苹果。
【样例 2】
见选手目录下的 apple/apple2.in 与 apple/apple2.ans。
【数据范围】
对于所有测试数据有:1 ≤ n ≤ 109。
测试点 n ≤ 特殊性质 1∼2 10 无
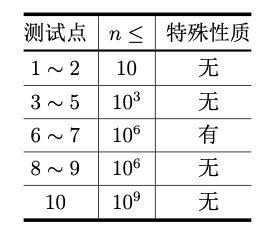
特殊性质:小苞第一天就取走编号为 n 的苹果。
公路(road)
【题目描述】
小苞准备开着车沿着公路自驾。
公路上一共有n个站点,编号为从1到n。其中站点i与站点i+1的距离为vi 公 里。
公路上每个站点都可以加油,编号为 i 的站点一升油的价格为 ai 元,且每个站点 只出售整数升的油。
小苞想从站点 1 开车到站点 n,一开始小苞在站点 1 且车的油箱是空的。已知车的 油箱足够大,可以装下任意多的油,且每升油可以让车前进 d 公里。问小苞从站点 1 开 到站点 n,至少要花多少钱加油?
【输入格式】
从文件 road.in 中读入数据。
输入的第一行包含两个正整数 n 和 d,分别表示公路上站点的数量和车每升油可以 前进的距离。
输入的第二行包含 n − 1 个正整数 v1, v2 . . . vn−1,分别表示站点间的距离。
输入的第二行包含 n 个正整数 a1, a2 . . . an,分别表示在不同站点加油的价格。
【输出格式】
输出到文件 road.out 中。
输出一行,仅包含一个正整数,表示从站点 1 开到站点 n,小苞至少要花多少钱加 油。
【样例 1 输入】
54
10101010 3 98965
【样例 1 输出】
79
【样例 1 解释】
最优方案下:小苞在站点 1 买了 3 升油,在站点 2 购买了 5 升油,在站点 4 购买 了 2 升油。
【样例 2】
见选手目录下的 road/road2.in 与 road/road2.ans。
【数据范围】
对于所有测试数据保证:1≤n≤105,1≤d≤105,1≤vi ≤105,1≤ai ≤105。
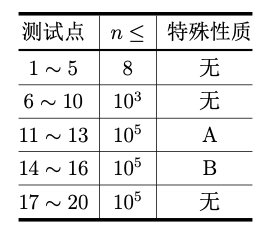
特殊性质 A:站点 1 的油价最低。
特殊性质B:对于所有1 ≤ i < n,vi 为d的倍数。
一元二次方程(uqe)
【题目背景】
众所周知,对一元二次方程 ax2 + bx + c = 0, (a ̸= 0),可以用下述方式求实数解: • 计算 ∆ = b2 − 4ac,则:
1. 若 ∆ < 0,则该一元二次方程无实数解;
2. 否则 ∆ ≥ 0,此时该一元二次方程有两个实数解 x1,2 = −b± ∆ ;
解互异。
例如:
• x2 +x+1=0无实数解,因为∆=12 −4×1×1=−3<0; • x2 −2x+1 = 0有两相等实数解x1,2 = 1;
• x2 −3x+2 = 0有两互异实数解x1 = 1,x2 = 2;
在题面描述中 a 和 b 的最大公因数使用 gcd(a, b) 表示。例如 12 和 18 的最大公因 数是 6,即 gcd(12, 18) = 6。
【题目描述】
现在给定一个一元二次方程的系数 a, b, c,其中 a, b, c 均. 为. 整. 数. 且. a ̸= 0。你需要判 断一元二次方程 ax2 + bx + c = 0 是否有实数解,并按要求的格式输出。
在.本.题.中.输.出.有.理.数. v 时.须.遵.循.以.下.规.则.:
· 由有理数的定义,存在唯. 一. 的两个整数 p 和 q,满足 q > 0,gcd(p, q) = 1 且
v = pq 。
· 若. q = 1,则. 输. 出. {p};否. 则. 输. 出. {p}/{q};其中 {n} 代表整数 n 的值;
· 例如:
– 当 v = −0.5 时,p 和 q 的值分别为 −1 和 2,则应输出 ‐1/2; – 当 v = 0 时,p 和 q 的值分别为 0 和 1,则应输出 0。
对. 于. 方. 程.的.求.解.,分.两.种.情.况. 讨. 论.:
1. 若 ∆ = b2 − 4ac < 0,则表明方程无实数解,此时你应当输出 NO;
2. 否则 ∆ ≥ 0,此时方程有两解(可能相等),记其中较. 大. 者. 为 x,则:
(1). 若 x 为有理数,则按有理数的格式输出 x。 (2).否则根据上文公式,x可以被唯.一.表示为x=q +q√r的形式,其中:
• q1,q2为有理数,且q2 >0;
• r为正整数且r>1,且不存在正整数d>1使d2|r(即r不应是d2的倍数);
此时:
1. 若 q1 ̸= 0,则按照有理数的格式输出 q1,并再输出一个加号 +; 2. 否则跳过这一步输出;
随后:
1. 若 q2 = 1,则输出 sqrt({r});
2. 否则若 q2 为整数,则输出 {q2}*sqrt({r});
3. 否则若 q3 = 1 为整数,则输出 sqrt({r})/{q3}; q2
4.否则可以证明存在唯一整数c,d满足c,d>1,gcd(c,d)=1且q2 =dc,此时 输出 {c}*sqrt({r})/{d};
上述表示中 {n} 代表整数 n 的值,详见样例。 如果方程有实数解,则按要求的格式输出两个实数解中的较大者。否则若方程没有
实数解,则输出 NO。
【输入格式】
从文件 uqe.in 中读入数据。
输入的第一行包含两个正整数 T , M ,分别表示方程数和系数绝对值的上界; 接下来 T 行,每行包含三个整数 a, b, c。
【输出格式】
输出到文件 uqe.out 中。
输出 T 行,每行包含一个字符串,表示对应询问的答案,格式如题面所述。 每. 行. 输. 出.的.字.符. 串. 中.间.不.应.包. 含. 任.何.空.格.。
【样例 1 输入】
9 1000
1 ‐1 0
‐1‐1‐1 4 1 ‐2 1
1 5 4
4 4 1
1 0‐432
1 ‐3 1
2 ‐4 1
1 7 1
【样例 1 输出】
1
NO
1
‐1
‐1/2
12*sqrt(3)
3/2+sqrt(5)/2
1+sqrt(2)/2
‐7/2+3*sqrt(5)/2
【样例 2】
见选手目录下的 uqe/uqe2.in 与 uqe/uqe2.ans。
【数据范围】
对于所有测试数据有:1 ≤ T ≤ 5000,1 ≤ M ≤ 103,|a|, |b|, |c| ≤ M,a ̸= 0。
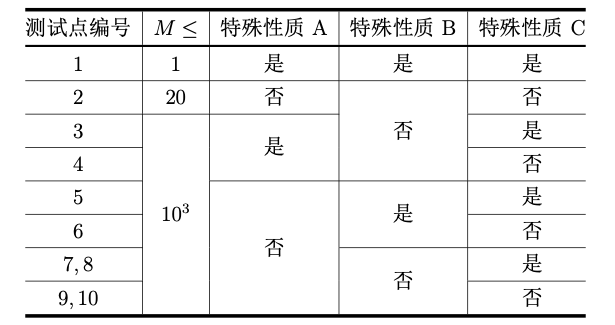
其中:
• 特殊性质A:保证b = 0;
• 特殊性质B:保证c = 0;
• 特殊性质 C:如果方程有解,那么方程的两个解都是整数。
旅游巴士(bus)
【题目描述】
小 Z 打算在国庆假期期间搭乘旅游巴士去一处他向往已久的景点旅游。
旅游景点的地图共有 n 处地点,在这些地点之间连有 m 条道路。其中 1 号地点为 景区入口,n 号地点为景区出口。我们把一天当中景区开门营业的时间记为 0 时刻,则 从 0 时刻起,每间隔 k 单位时间便有一辆旅游巴士到达景区入口,同时有一辆旅游巴士 从景区出口驶离景区。
所有道路均只能单. 向. 通. 行. 。对于每条道路,游客步行通过的用时均为恰好 1 单位时 间。
小 Z 希望乘坐旅游巴士到达景区入口,并沿着自己选择的任意路径走到景区出口, 再乘坐旅游巴士离开,这意味着他到达和离开景区的时间都必须是 k 的. 非. 负. 整. 数. 倍. 。由 于节假日客流众多,小. Z 在.坐.旅.游.巴.士.离.开.景.区.前.只.想.一.直.沿.着.景.区.道.路.移.动.,而.不. 想.在.任.何.地.点.(包.括.景.区.入.口.和.出.口.)或.者.道.路.上.逗.留.。
出发前,小 Z 忽然得知:景区采取了限制客流的方法,对于每条道路均设置了一个 “开放时间”ai,游客只有不. 早. 于. ai 时. 刻. 才能通过这条道路。
请你帮助小 Z 设计一个旅游方案,使得他乘坐旅游巴士离开景区的时间尽量地早。 【输入格式】
从文件 bus.in 中读入数据。
输入的第一行包含 3 个正整数 n, m, k,表示旅游景点的地点数、道路数,以及旅游 巴士的发车间隔。
输入的接下来 m 行,每行包含 3 个非负整数 ui, vi, ai,表示第 i 条道路从地点 ui 出发,到达地点 vi,道路的“开放时间”为 ai。
【输出格式】
输出到文件 bus.out 中。
输出一行,仅包含一个整数,表示小 Z 最早乘坐旅游巴士离开景区的时刻。如果不 存在符合要求的旅游方案,输出 ‐1。
【样例 1 输入】
5 5 3
1 2 0
2 5 1
1 3 0
3 4 3
4 5 1
【样例 1 输出】
6
【样例 1 解释】
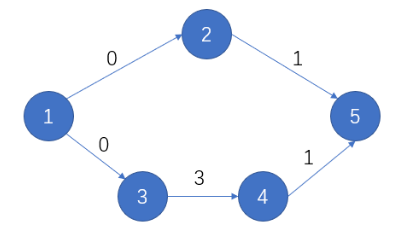
图1: 样例1示例
小Z可以在3时刻到达景区入口,沿1 → 3 → 4 → 5的顺序走到景区出口,并在 6 时刻离开。
【样例 2】
见选手目录下的 bus/bus2.in 与 bus/bus2.ans。
【数据范围】
对于所有测试数据有:2≤n≤104,1≤m≤2×104,1≤k≤100,1≤ui,vi ≤n, 0≤ai ≤106。