扑克牌(poker)

【题目描述】

小 P 从同学小 Q 那儿借来一副 n 张牌的扑克牌。

本题中我们不考虑大小王，此时每张牌具有两个属性:花色和点数。花色共有 4 种: 方片、草花、红桃和黑桃。点数共有 13 种，从小到大分别为 A 2 3 4 5 6 7 8 9 T J Q K。注意:点数 10 在本题中记为 T。

我们称一副扑克牌是完.整.的，当且仅当对于每一种花色和每一种点数，都恰.好有一 张牌具有对应的花色和点数。由此，一副完整的扑克牌恰好有 4 × 13 = 52 张牌。以下图片展示了一副完整的扑克牌里所有的 52 张牌。

小 P 借来的牌可能不是完整的，为此小 P 准备再向同学小 S 借若干张牌。可以认 为小 S 每种牌都有无限张，因此小 P 可以任意选择借来的牌。小 P 想知道他至少得向 小 S 借多少张牌，才能让从小 S 和小 Q 借来的牌中，可以选出 52 张牌构成一副完整的 扑克牌。

为了方便你的输入，我们使用字符 D 代表方片，字符 C 代表草花，字符 H 代表红 桃，字符 S 代表黑桃，这样每张牌可以通过一个长度为 2 的字符串表示，其中第一个字 符表示这张牌的花色，第二个字符表示这张牌的点数，例如 CA 表示草花 A，ST 表示黑 桃 T(黑桃 10)。

【输入格式】

从文件 poker.in 中读入数据。
输入的第一行包含一个整数 n 表示牌数。
接下来 n 行:
每行包含一个长度为 2 的字符串描述一张牌，其中第一个字符描述其花色，第二个字符描述其点数。

【输出格式】

输出到文件 poker.out 中。
输出一行一个整数，表示最少还需要向小 S 借几张牌才能凑成一副完整的扑克牌。

【样例 1 输入】 

1
SA

【样例 1 输出】 

51

【样例 1 解释】
这一副牌中包含一张黑桃 A，小 P 还需要借除了黑桃 A 以外的 51 张牌以构成一副完整的扑克牌。

【样例 2 输入】

4
DQ
H3
DQ
DT

【样例 2 输出】

49

【样例 2 解释】
这一副牌中包含两张方片 Q、一张方片 T(方片 10)以及一张红桃 3，小 P 还需要借除了红桃 3、方片 T 和方片 Q 以外的 49 张牌。 

【样例 3】

见选手目录下的 poker/poker3.in 与 poker/poker3.ans。

【样例 3 解释】

这一副扑克牌是完整的，故不需要再借任何牌。
该样例满足所有牌按照点数从小到大依次输入，点数相同时按照方片、草花、红桃、 黑桃的顺序依次输入。

【数据范围】

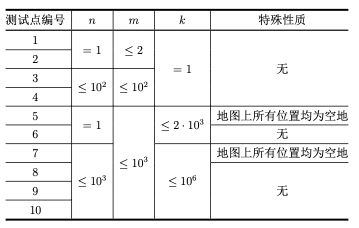
对于所有测试数据，保证:1 ≤ n ≤ 52，输入的 n 个字符串每个都代表一张合法的 扑克牌，即字符串长度为 2，且第一个字符为 D C H S 中的某个字符，第二个字符为 A 2 3 4 5 6 7 8 9 T J Q K 中的某个字符。

特殊性质 A:保证输入的 n 张牌两两不同。

特殊性质 B:保证所有牌按照点数从小到大依次输入，点数相同时按照方片、草花、 红桃、黑桃的顺序依次输入。

地图探险(explore)

【题目描述】

小 A 打算前往一片丛林去探险。丛林的地理环境十分复杂，为了防止迷路，他先派 遣了一个机器人前去探路。

丛林的地图可以用一个 n 行 m 列的字符表来表示。我们将第 i 行第 j 列的位置的 坐标记作 (i, j)(1 ≤ i ≤ n, 1 ≤ j ≤ m)。如果这个位置的字符为 x，即代表这个位置上有 障碍，不可通过。反之，若这个位置的字符为 .，即代表这个位置是一片空地，可以通 过。

这个机器人的状态由位置和朝向两部分组成。其中位置由坐标 (x, y)(1 ≤ x ≤ n, 1 ≤ y ≤ m) 刻画，它表示机器人处在地图上第 x 行第 y 列的位置。而朝向用一个 0 ∼ 3 的 整数d表示，其中d = 0代表向东，d = 1代表向南，d = 2代表向西，d = 3代表向北。

初始时，机器人的位置为 (x0, y0)，朝向为 d0。保. 证. 初. 始. 时. 机. 器. 人. 所. 在. 的. 位. 置. 为. 空. 地.。接下来机器人将要进行k次操作。每一步，机器人将按照如下的模式操作:

1. 假设机器人当前处在的位置为 (x, y)，朝向为 d。则它的方向上的下一步的位 置 (x′,y′) 定义如下:若 d = 0，则令 (x′,y′) = (x,y + 1)，若 d = 1，则令 (x′,y′) = (x + 1,y)，若 d = 2，则令 (x′,y′) = (x,y − 1)，若 d = 3，则令 (x′,y′) = (x − 1,y)。

2. 接下来，机器人判断它下一步的位置是否在地图内，且是否为空地。具体地说， 它判断 (x′,y′) 是否满足 1 ≤ x′ ≤ n,1 ≤ y′ ≤ m，且 (x′,y′) 位置上是空地。如果 条件成立，则机器人会向前走一步。它新的位置变为 (x′, y′)，且朝向不变。如果 条件不成立，则它会执行“向右转”操作。也就是说，令 d′ = (d + 1) mod 4(即 d + 1 除以 4 的余数)，且它所处的位置保持不变，但朝向由 d 变为 d′。

小 A 想要知道，在机器人执行完 k 步操作之后，地图上所有被机器人经过的位置 (包括起始位置)有几个。

【输入格式】

从文件 explore.in 中读入数据。
本. 题. 有. 多.组.测.试. 数. 据.。
输入的第一行包含一个正整数 T，表示数据组数。
接下来包含 T 组数据，每组数据的格式如下:
第一行包含三个正整数 n, m, k。其中 n, m 表示地图的行数和列数，k 表示机器人执行操作的次数。

第二行包含两个正整数 x0, y0 和一个非负整数 d0。
接下来 n 行，每行包含一个长度为 m 的字符串。保证字符串中只包含 x 和 . 两个字符。其中，第 x 行的字符串的第 y 个字符代表的位置为 (x, y)。这个位置是 x 即代表 它是障碍，否则代表它是空地。数据保证机器人初始时所在的位置为空地。

【输出格式】

输出到文件 explore.out 中。

对于每组数据:输出一行包含一个正整数，表示地图上所有被机器人经过的位置 (包括起始位置)的个数。

【样例 1 输入】

2
1 5 4 
1 1 2
....x
5 5 20
1 1 0
.....
.xxx.
.x.x.
..xx.
x....

【样例 1 输出】 

3
13

【样例 1 解释】

  该样例包含两组数据。对第一组数据，机器人的状态以如下方式变化:

1、初始时，机器人位于位置 (1, 1)，方向朝西(用数字 2 代表)。

2、第一步，机器人发现它下一步的位置 (1, 0) 不在地图内，因此，它会执行“向右转”操作。此时，它的位置仍然为 (1, 1)，但方向朝北(用数字 3 代表)。

3、第二步，机器人发现它下一步的位置 (0, 1) 不在地图内，因此，它仍然会执行“向右转”操作。此时，它的位置仍然为 (1, 1)，但方向朝东(用数字 0 代表)。

4、第三步，机器人发现它下一步的位置 (1, 2) 在地图内，且为空地。因此，它会向东走一步。此时，它的位置变为 (1, 2)，方向仍然朝东。

5、第四步，机器人发现它下一步的位置 (1, 3) 在地图内，且为空地。因此，它会向东走一步。此时，它的位置变为 (1, 3)，方向仍然朝东。

因此，四步之后，机器人经过的位置有三个，分别为 (1, 1), (1, 2), (1, 3)。

对第二组数据，机器人依次执行的操作指令为:向东走到 (1, 2)，向东走到 (1, 3)， 向东走到 (1, 4)，向东走到 (1, 5)，向右转，向南走到 (2, 5)，向南走到 (3, 5)，向南走到 (4, 5)，向南走到 (5, 5)，向右转，向西走到 (5, 4)，向西走到 (5, 3)，向西走到 (5, 2)，向 右转，向北走到 (4, 2)，向右转，向右转，向南走到 (5, 2)，向右转，向右转。

【样例 2】
见选手目录下的 explore/explore2.in 与 explore/explore2.ans。

该样例满足第 3 ∼ 4 个测试点的限制条件。 

【样例 3】

见选手目录下的 explore/explore3.in 与 explore/explore3.ans。 该样例满足第 5 个测试点的限制条件。

【样例 4】
见选手目录下的 explore/explore4.in 与 explore/explore4.ans。

该样例满足第 6 个测试点的限制条件。 

【样例 5】

见选手目录下的 explore/explore5.in 与 explore/explore5.ans。 该样例满足第 8 ∼ 10 个测试点的限制条件。

【数据范围】

对于所有测试数据，保证:1≤T ≤5,1≤n,m≤103,1≤k≤106,1≤x0 ≤n,1≤ y0 ≤ m, 0 ≤ d0 ≤ 3，且机器人的起始位置为空地。

小木棍(sticks)

【题目描述】

小 S 喜欢收集小木棍。在收集了 n 根长度相等的小木棍之后，他闲来无事，便用它 们拼起了数字。用小木棍拼每种数字的方法如下图所示。

图 2: 每种数字的小木棍拼法

现在小 S 希望拼出一个正. 整数，满足如下条件:
• 拼出这个数恰. 好. 使用 n 根小木棍;
• 拼出的数没有前导 0;
• 在满足以上两个条件的前提下，这个数尽可能小。

小 S 想知道这个数是多少，可 n 很大，把木棍整理清楚就把小 S 折腾坏了，所以 你需要帮他解决这个问题。如果不存在正整数满足以上条件，你需要输出 ‐1 进行报告。

【输入格式】

从文件 sticks.in 中读入数据。
本. 题. 有. 多.组.测.试. 数. 据.。 输入的第一行包含一个正整数 T，表示数据组数。 接下来包含 T 组数据，每组数据的格式如下: 一行包含一个整数 n，表示木棍数。

【输出格式】

输出到文件 sticks.out 中。 对于每组数据:输出一行，如果存在满足题意的正整数，输出这个数;否则输出 ‐1。

【样例 1 输入】

5
1
2
3
6
18

【样例 1 输出】

‐1
1 
7
6
208

【样例 1 解释】

• 对于第一组测试数据，不存在任何一个正整数可以使用恰好一根小木棍摆出，故 输出 ‐1。

• 对于第四组测试数据，注意0并不是一个满足要求的方案。摆出9、41以及111 都恰好需要 6 根小木棍，但它们不是摆出的数最小的方案。

• 对于第五组测试数据，摆出 208 需要 5 + 6 + 7 = 18 根小木棍。可以证明摆出任 何一个小于 208 的正整数需要的小木棍数都不是 18。注意尽管拼出 006 也需要 18 根小木棍，但因为这个数有前导零，因此并不是一个满足要求的方案。

  【数据范围】

  对于所有测试数据，保证:1 ≤ T ≤ 50，1 ≤ n ≤ 105。

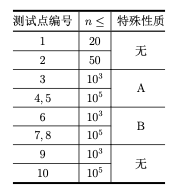
特殊性质A:保证n是7的倍数且n ≥ 100。

特殊性质 B:保证存在整数 k 使得 n = 7k + 1，且 n ≥ 100。

接龙(chain)

【题目描述】

在玩惯了成语接龙之后，小 J 和他的朋友们发明了一个新的接龙规则。

总共有 n 个人参与这个接龙游戏，第 i 个人会获得一个整数序列 Si 作为他的词库。 一次游戏分为若干轮，每一轮规则如下:

• n 个人中的某个人 p 带着他的词库 Sp 进行接龙。若这不是游戏的第一轮，那么 这一轮进行接龙的人不能与上一轮相同，但可以与上上轮或更往前的轮相同。

• 接龙的人选择一个长度在 [2, k] 的 Sp 的连续子序列 A 作为这一轮的接. 龙. 序. 列. ， 其中 k 是给定的常数。若这是游戏的第一轮，那么 A 需要以元素 1 开头，否则 A 需要以上一轮的接龙序列的最后一个元素开头。

– 序列 A 是序列 S 的连续子序列当且仅当可以通过删除 S 的开头和结尾的 若干元素(可以不删除)得到 A。

为了强调合作，小 J 给了 n 个参与游戏的人 q 个任务，第 j 个任务需要这 n 个人 进行一次游戏，在这次游戏里进行恰好 rj 轮接龙，且最后一轮的接龙序列的最后一个 元素恰好为 cj。为了保证任务的可行性，小 J 请来你判断这 q 个任务是否可以完成的， 即是否存在一个可能的游戏过程满足任务条件。

【输入格式】

从文件 chain.in 中读入数据。
本. 题. 有. 多.组.测.试. 数. 据.。
输入的第一行包含一个正整数 T，表示数据组数。
接下来包含 T 组数据，每组数据的格式如下:
第一行包含三个整数 n, k, q，分别表示参与游戏的人数、接龙序列长度上限以及任

务个数。
接下来 n 行:

第i行包含(li +1)个整数li,Si,1,Si,2,··· ,Si,li，其中第一个整数li 表示序列Si 的 长度，接下来 li 个整数描述序列 Si。

接下来 q 行:
第 j 行包含两个整数 rj , cj ，描述一个任务。

【输出格式】

输出到文件 chain.out 中。 对于每个任务:输出一行包含一个整数，若任务可以完成输出 1，否则输出 0。

【样例 1 输入】

1
3 3 7
5 1 2 3 4 1
3 1 2 5
3 5 1 6
1 2
1 4
2 4
3 4
6 6 
1 1
7 7

【样例 1 输出】

1
0
1
0
1
0
0

【样例 1 解释】

在下文中，我们使用 {Ai} = {A1, A2, · · · , Ar} 表示一轮游戏中所有的接龙序列， {pi} = {p1, p2, · · · , pr} 表示对应的接龙的人的编号。由于所有字符均为一位数字，为了 方便我们直接使用数字字符串表示序列。

• 对于第一组询问，p1 = 1、A1 = 12 是一个满足条件的游戏过程。

• 对于第二组询问，可以证明任务不可完成。注意 p1 = 1、A1 = 1234 不是合法的

  游戏过程，因为此时 |A1| = 4 > k。

• 对于第三组询问，{pi} = {2, 1}、{Ai} = {12, 234} 是一个满足条件的游戏过程。

• 对于第四组询问，可以证明任务不可完成。注意 {pi} = {2, 1, 1}、{Ai} = {12, 23, 34}

  不是一个合法的游戏过程，因为尽管所有的接龙序列长度均不超过 k，但第二轮 和第三轮由同一个人接龙，不符合要求。

• 对于第五组询问，{pi} = {1, 2, 3, 1, 2, 3}、{Ai} = {12, 25, 51, 12, 25, 516} 是一个 满足条件的游戏过程。

• 对于第六组询问，可以证明任务不可完成。注意每个接龙序列的长度必须大于等 于 2，因此 A1 = 1 不是一个合法的游戏过程。

• 对于第七组询问，所有人的词库均不存在字符 7，因此任务显然不可完成。 

  【样例 2】

  见选手目录下的 chain/chain2.in 与 chain/chain2.ans。 该样例满足测试点 1 的特殊性质。

  【样例 3】
  见选手目录下的 chain/chain3.in 与 chain/chain3.ans。

  该样例满足测试点 2 的特殊性质。 

  【样例 4】

  见选手目录下的 chain/chain4.in 与 chain/chain4.ans。

  该样例满足特殊性质 A，其中前两组测试数据满足 n ≤ 1000、r ≤ 10、单组测试数 据内所有词库的长度和 ≤ 2000、q ≤ 1000。

  【样例 5】

  见选手目录下的 chain/chain5.in 与 chain/chain5.ans。

  该样例满足特殊性质 B，其中前两组测试数据满足 n ≤ 1000、r ≤ 10、单组测试数 据内所有词库的长度和 ≤ 2000、q ≤ 1000。

  【样例 6】

  见选手目录下的 chain/chain6.in 与 chain/chain6.ans。

  该样例满足特殊性质 C，其中前两组测试数据满足 n ≤ 1000、r ≤ 10、单组测试数 据内所有词库的长度和 ≤ 2000、q ≤ 1000。

  【数据范围】

  对于所有测试数据，保证:
  • 1 ≤ T ≤ 5;
  • 1≤n≤105，2≤k≤2×105，1≤q≤105; • 1≤li ≤2×105，1≤Si,j ≤2×105;

        • 1≤rj ≤102，1≤cj ≤2×105;

        • 设 ∑ l 为单. 组. 测. 试. 数. 据. 内. 所有 li 的和，则 ∑ l ≤ 2 × 105。

特殊性质 A:保证 k = 2 × 105。
特殊性质 B:保证 k ≤ 5。
特殊性质 C:保证在单组测试数据中，任意一个字符在词库中出现次数之和均不超过 5。